マルテンパーとは

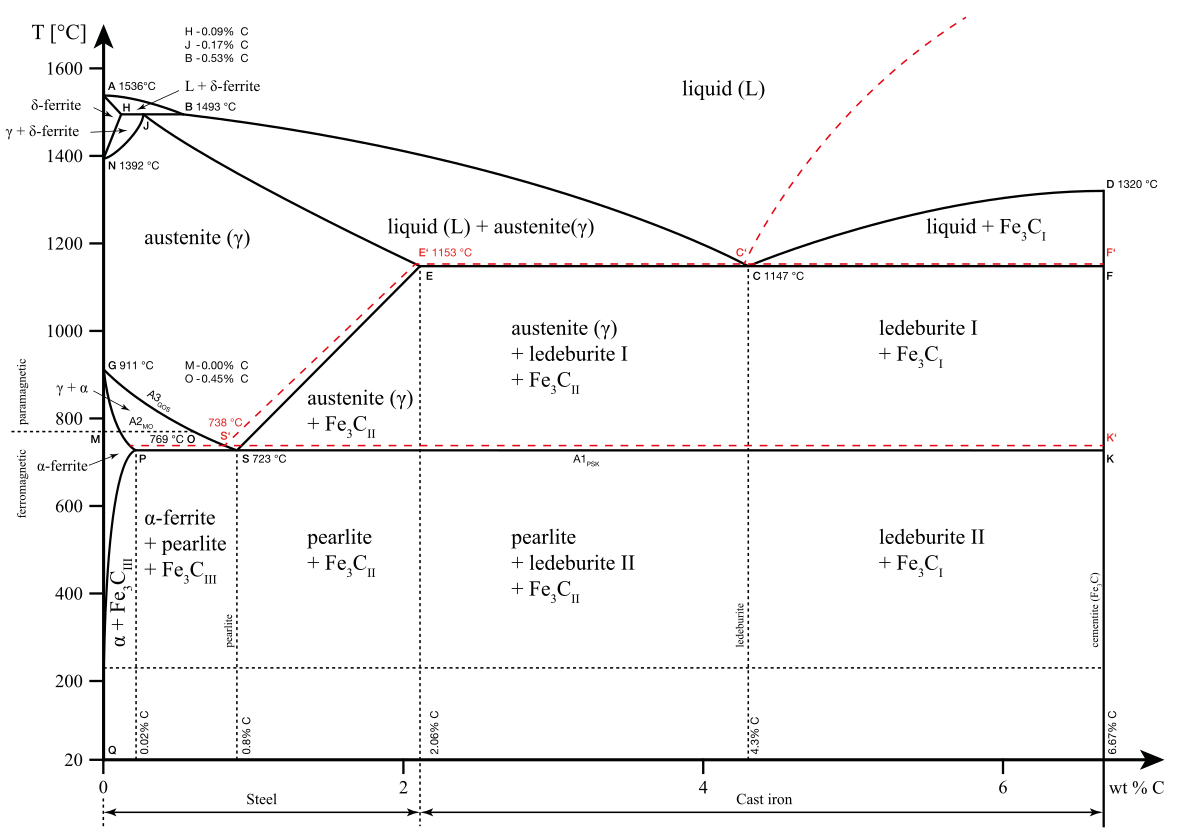
こんばんは。 まず、これは「冷却速度」に関係してきます。 金属の熱処理学の場合は、共析鋼とは言っても、冷却速度によって全く違う変態、組織構成を持つということを念頭においてください。 共析鋼C0. しかし、マルテンサイト変態点に到達すると、「過冷却」が打ち破られ、マルテンサイトに変態しはじめます。 この場合、面心立法格子の過冷オーステナイトが、マルテンサイトの完全な体心立法格子に変態を起こし、急激な体積膨張をおこします。 Mf点は冷却速度によらず不変です。 つまりMfにはマルテンサイト変態が終了しますので、マルテンサイト変態による膨張は起きません・・・と言いたいところですが・・・・実際には室温付近までマルテンサイト変態が続き、膨張が継続します。 サンプルの深部温度が表面より高いと言う意見もありますが、私は過冷却から析出の場合、確率的に結晶ごとにムラがあるためだと思います) 共析鋼より高炭素な過共析鋼(C0. (またMf点の降下で普通の焼入れをしても、室温より下でマルテンサイト変態をせず残っているオーステナイトを「残留オーステナイト」と言います) また合金鋼種が変わると、メカニズム、各論が変化しますのでその時は、別の質問でお願いします。 A ベストアンサー 変態という現象が分かりますか? 金属材料ではbcc構造やfcc構造などをとりますが、このような構造が変化することを変態といいます。 変態する理由としては、温度によって安定な状態が異なるからであり、ギブスの自由エネルギーから知ることができます。 その変態のメカニズムですが、一般に高温からゆっくりと冷却した場合は、拡散変態が起こります。 変態とは上でも述べたように構造が変化するわけですから、原子が拡散することによって変態が起こる拡散変態はイメージしやすいと思います。 それに対して、高温から急冷した場合には無拡散変態を起こします。 即ち拡散を伴わずに原子が隣同士くっついたままひずむことによって構造が変化します。 拡散という現象は、原子が(熱)エネルギーを得ることによって起こるため急冷したときは、必要な熱エネルギーが得られず、拡散できません。 しかし構造的には変化した方が安定な場合、変態温度からの過冷度を変態の駆動力として無拡散で変態します。 また拡散できるためのエネルギーは原子の種類によって異なります(侵入型元素だったり置換型元素だったり母合金と結合力が強かったり)。 そのため同じ冷却速度でも合金組成によっては無拡散変態をしたり、しなかったり、一部だけ無拡散変態をしたりします。 サブゼロ処理とは、急冷後の組織全面を、無拡散変態で得られるマルテンサイトにするために行なうもので、材料の均一化、体積変化(膨張)の抑制のために行ないます。 変態という現象が分かりますか? 金属材料ではbcc構造やfcc構造などをとりますが、このような構造が変化することを変態といいます。 変態する理由としては、温度によって安定な状態が異なるからであり、ギブスの自由エネルギーから知ることができます。 その変態のメカニズムですが、一般に高温からゆっくりと冷却した場合は、拡散変態が起こります。 変態とは上でも述べたように構造が変化するわけですから、原子が拡散することによって変態が起こる拡散変態はイメージしやすいと思います。 それに対して、... A ベストアンサー 「格子定数」「ミラー指数」などと出てくると構えてしまいますが、この問題の本質は3次元空間での簡単な幾何であり、高校生の数学の範囲で解くことができます。 なぜわざわざ逆数にするの? という辺りから話がこんがらがることがしばしばです。 大雑把に言えばミラー指数は法線ベクトルのようなものです。 特に立方晶であれば法線ベクトルと全く同じになります。 すなわち立方晶の 111 面の法線ベクトルは 1,1,1 ですし、 100 面の法線ベクトルは 1,0,0 です。 法線ベクトルなら「ミラー指数」よりずっと親しみがあり解けそうな気分になると思います。 さて hkl 面に相当する平面の方程式を一つ考えてみましょう。 0,0,0 を通る平面で法線ベクトルは h,k,l です。 これに平行な、隣の平面の式はどうでしょうか。 点と直線の距離の公式を使わなくとも、次のようにすれば求められます。 原点Oから法線ベクトル h,k,l の方向に進み、平面 2a とぶつかった点をA p,q,r とします。 OAの長さは面間隔dにほかならないので、 3 式が得られたことになります。 bokoboko777さん、これでいかがでしょうか。 例えば 111 面とは言いますが 222 面なる表現は使いません。 37aや5aにならないのは何故か は以下のように説明されます。 この平面は少なくとも一つの格子点を通過する必要があります。 その点を x0,y0,z0 とします。 h,k,lはミラー指数の定義から整数です。 すると右辺のCも少なくともaの整数倍でなければなりません。 このことは次の命題と等価です。 p, 2p, 3p,... , q-1 pをqで順に割った際の余りを考えてみる。 pをqで割った際の余りをr[1] 整数 とする。 同様に2pで割った際の余りをr[2]・・・とする。 よって命題は成り立つ。 ただここまで詳しく説明する必要はないでしょう。 207. 「講義資料」から「テキスト 第3章」をダウンロードして読んでみてください。 207. なぜわざわざ逆数にするの? という辺りから話がこんがらがることがしばしばです。 大雑把に言えばミラー指数は法線ベクトルのようなものです。 特に立方晶であれば法線ベ... A ベストアンサー 前回拙い回答で混乱を招いてしまったかもしれません。 SUS304などのオーステナイト系ステンレス鋼は、固溶化熱処理後、オーステナイト相が生成されますが、 熱力学的安定性が高くないため、準安定オーステナイトと呼ばれています。 例えば、SUS304材を冷間深絞り加工しますと、 素材にエネルギーが加えられ、より安定な組織であるマルテンサイトに変態します。 この様に冷間加工する事により生成しますから、これを防ぐには温間加工(予め80~100度程度に材料を加熱し加工する)事で生成が抑えられます。 3については勉強不足でお役に立てません申し訳ないです。 またこの様な金属に関する専門的な質問は「技術の森」と言うQ&Aサイトがありますから、そこの「金属」のカテゴリーで聞いてみるのも良いと思います。 nc-net. SUS304などのオーステナイト系ステンレス鋼は、固溶化熱処理後、オーステナイト相が生成されますが、 熱力学的安定性が高くないため、準安定オーステナイトと呼ばれています。 例えば、SUS304材を冷間深絞り加工しますと、 素材にエネルギーが加えられ、より安定な組織であるマルテンサイトに変態します。 この様に冷間加工する事により生成しますから、これを防ぐには温間加工(予め80~100度程度に材料を加熱し加工する)事で生成が抑えられます。 A ベストアンサー 平衡状態図はその名の通り温度Tのときの鉄中の炭素濃度がx%の平衡状態のときの組織が示してあります。 平衡状態なのでその温度にずーーーーっと保持したときの組織と考えることができます。 ここからゆーーーっくり冷却(徐冷という)した場合の組織を平衡状態図から予測できます。 ここで徐冷であるのは平衡変態(平衡状態を保ったまま変態)しているとみなすためであり、また実際、徐冷ならほぼ平衡変態になります。 炭素濃度が0. まず0. さらに冷却していくと二本目の線と交わります。 これより冷却しても相、組織は変わりません。 次に先に炭素濃度が1. 基本的には先ほどと同様です。 析出する量はこの一本目の線と炭素濃度6. 7%の縦線の間のてこの法則で求まります。 さらに冷却すると先ほどと同じ二本目の線と交差します。 ここで二本目の線より下で0. 最後に0. 以上長くなりましたが、相比や組織比について、冷却速度が速くなった場合について等、補足が必要な場合には遠慮なく言って下さい。 平衡状態図はその名の通り温度Tのときの鉄中の炭素濃度がx%の平衡状態のときの組織が示してあります。 平衡状態なのでその温度にずーーーーっと保持したときの組織と考えることができます。 ここからゆーーーっくり冷却(徐冷という)した場合の組織を平衡状態図から予測できます。 ここで徐冷であるのは平衡変態(平衡状態を保ったまま変態)しているとみなすためであり、また実際、徐冷ならほぼ平衡変態になります。 炭素濃度... A ベストアンサー >メッキ鋼板、ステンレス(鉄にクロム、ニッケルを混ぜた?もの)、チタン合金等は..... 一般的には不純物等による金属間化合物、酸化物、炭化物等も含んでいます。 チタン合金:組成により、異なります。 Ti-Al-V系では固溶体かな?ただ、Ti-Alの間では、Ti3Al等の金属間化合物も存在するので、よくわかりません。 金属間化合物にも、化学量論組成からズレたものも存在します。 金属間化合物を作っているか/固溶体かは 相図 phase Diagram を見れば判ります。 但し、相図は十分な時間経過の後の安定な状態です。 急冷等にて作ったものは非安定相が含まれることがあり、この場合は判りません Q 還元雰囲気下でのガラス作製を行おうとしています。 文献によると、活性炭素粉末を、溶融試料(SiO2-CaO-Al2O3を調製)とは混合しない状態で大気雰囲気炉内に設置することで、還元雰囲気とするとありました。 また炉内を、大気雰囲気ではなく、不活性(窒素)雰囲気とした際にも、炭素による還元効果は得られるのでしょうか。 宜しくお願いします。 A ベストアンサー 私と質問者さまは畑違いですが、炉を使うと言う共通点があります。 私は金属材料方面の人間です。 ブードア平衡図は、炉内CO濃度(%)と炉内温度(K)に比例して起きる「CO2+C=2CO」の可逆反応に着目したものです。 これは金属材料学で重視されているものです。 (異業種でも役に立つかと・・・) まず活性炭素粉末を、ほぼ同意義の立体構造を持たないグラファイト(カーボン)に置き換える事が出来ます。 つまり「COからCが遊離し、還元的雰囲気を形成する」と言うのが答えになります。 見つける自信が無かったのですが、幸い状態図を発見しましたのでURLの図を見てください。 特に(1)の線に注目して見てください。 jfe-21st-cf. 不活性ガス下で、大気圧中での昇華が認められるのは5100Kと言われています。 私は金属関係の方が専門なので経験者とさせてください。 つたない文面ですが、参考になれば。 私と質問者さまは畑違いですが、炉を使うと言う共通点があります。 私は金属材料方面の人間です。 ブードア平衡図は、炉内CO濃度(%)と炉内温度(K)に比例して起きる「CO2+C=2CO」の可逆反応に着目したものです。 これは金属材料学で重視されているものです。 (異業種でも役に立つかと... Q エクセルの統計関数で標準偏差を求める時、STDEVとSTDEVPがあります。 両者の違いが良くわかりません。 宜しかったら、恐縮ですが、以下の具体例で、『噛み砕いて』教えて下さい。 (例) セルA1~A13に1~13の数字を入力、平均値=7、STDEVでは3. 89444、STDEVPでは3. 741657となります。 また、平均値7と各数字の差を取り、それを2乗し、総和を取る 182 、これをデータの個数13で割る 14 、この平方根を取ると3. 741657となります。 では、STDEVとSTDEVPの違いは何なのでしょうか?統計のことは疎く、お手数ですが、サルにもわかるようご教授頂きたく、お願い致します。 A ベストアンサー データが母集団そのものからとったか、標本データかで違います。 また母集団そのものだったとしても(例えばクラス全員というような)、その背景にさらならる母集団(例えば学年全体)を想定して比較するような時もありますので、その場合は標本となります。 で標本データの時はSTDEVを使って、母集団の時はSTDEVPをつかうことになります。 公式の違いは分母がn-1(STDEV)かn(STDEVP)かの違いしかありません。 まぁ感覚的に理解するなら、分母がn-1になるということはそれだけ結果が大きくなるわけで、つまりそれだけのりしろを多くもって推測に当たるというようなことになります。 AとBの違いがあるかないかという推測をする時、通常は標本同士の検証になるわけですので、偏差を余裕をもってわざとちょっと大きめに見るということで、それだけ確証の度合いを上げるというわけです。 A ベストアンサー こんにちは。 kgfはSI単位ではないですが、質量の数値をそのまま重さとして考えることができるのがメリットですね。 >>> ある試験片に40kgの重りをつけた時の荷重は何Nをかけてあげると、重り40kgをつけたときの荷重と同等になるのでしょうか? なんか、日本語が変ですね。 「ある試験片に40kgの重りをつけた時の引っ張りの力は何Nの力で引っ張るのと同じですか?」 ということですか? ・・・であるとして、回答します。 40kgのおもりなので、「おもりにかかる重力」は40kgfです。 重力は万有引力の一種ですから、おもりにも試験片にも、地球からの重力はかかります。 しかし、試験片の片方が固定されているため、見かけ、無重力で、試験片だけに40kgfの力だけがかかっているのと同じ状況になります。 98」でいいのでしょうか? いえ。 1kgf = 9.8N ですね。 力だけでなく、引っ張り応力を求めたいのでしょうか。 そうであれば、400Nを断面積で割るだけです。 こんにちは。 kgfはSI単位ではないですが、質量の数値をそのまま重さとして考えることができるのがメリットですね。 >>> ある試験片に40kgの重りをつけた時の荷重は何Nをかけてあげると、重り40kgをつけたときの荷重と同等になるのでしょうか? なんか、日本語が変ですね。 「ある試験片に40kgの重りをつけた時の引っ張りの力は何Nの力で引っ張るのと同じですか?」 ということですか? ・・・であるとして、回答します。 40kgのおもりなので、「おもりにかかる重力」は40kg...
次の