平行 四辺 形 の 面積。 平行四辺形の面積の求め方【公式】

四角形の面積の求め方。公式とその仕組み【小学算数】｜アタリマエ！

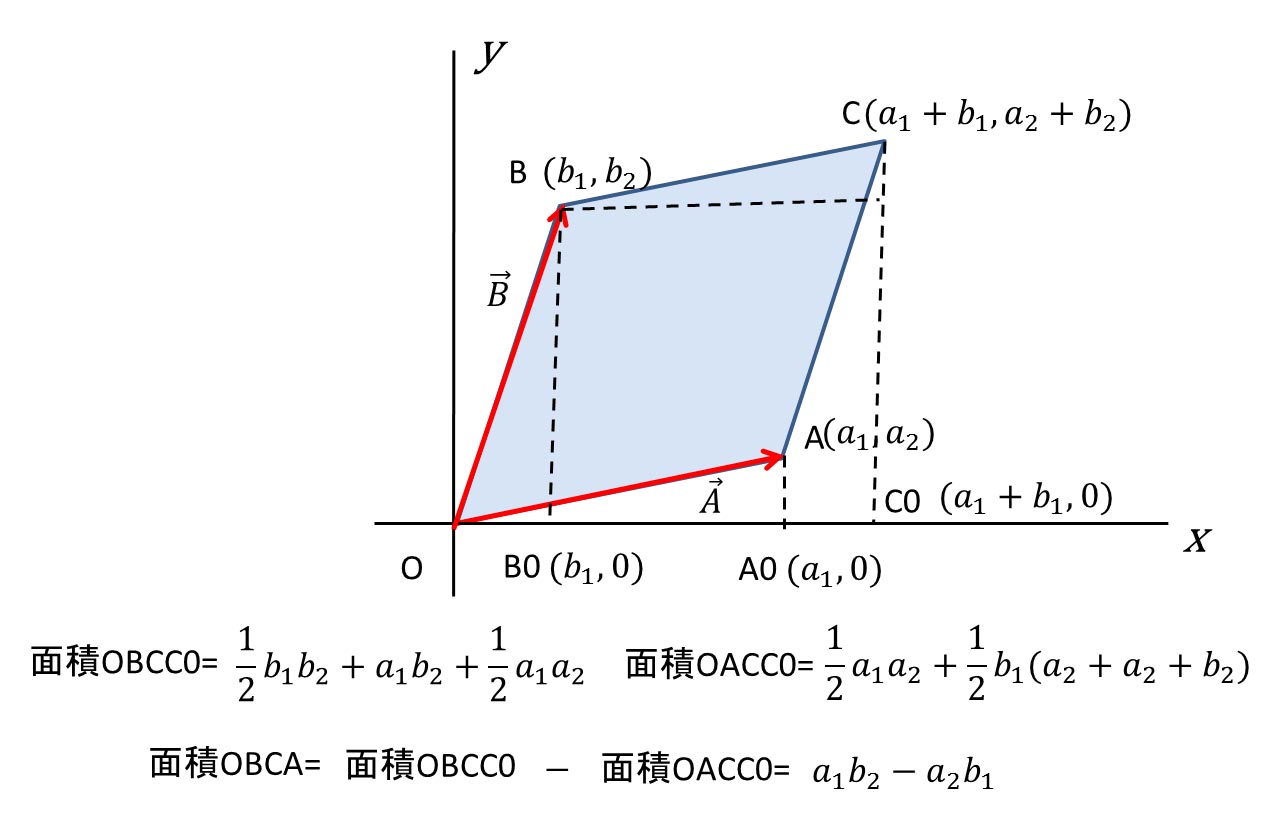
【面積ベクトルのまえに】ベクトルとは 先にも申し上げたように、「ベクトルとはベクトル空間の元である」というのが一般的な定義です。 そして、高校数学で扱うベクトルは「幾何ベクトル」と呼ばれる、ベクトルの概念の一部です。 幾何ベクトルにおいて最も大切なことは「『大きさ』と『向き』を持つ量である」ということです。 端的に言えば、 幾何ベクトルは矢印です。 一般に向きと大きさをもった量は、 有向線分と呼ばれる矢印で表すことができます。 例えば A地点から B地点へ直線的に向かうとき、 Aから Bへ矢印を引くことができます。 このとき、 Aを始点、 Bを終点といいます。 有向線分とベクトルの違いは、「位置を問題にするかどうか」であり、ベクトルは位置を問題にしません。 違う位置にあっても、「向き」と「大きさ」が同じであれば、同じベクトルであるとされます。 ですから、 （高校で扱う）ベクトルとは、「『大きさ』と『向き』だけをもつ量（平行移動できる）」といって問題ないでしょう。 有向線分 ABで表されるベクトルを と書きます。 ベクトルを座標平面上に置いたとき、 x座標成分と y座標成分に分けることができ、それぞれの成分を並べて のように表します。 これを ベクトルの成分表示と言います。 2次元の座標なら、ベクトルの成分表示は 2つの数で表されますが、 3次元なら のように 3つの数で表されます。 ベクトルを用いることで、図形問題をシンプルに扱うことができるようになります。 例えば、 2点 A、 Bにおいて、線分 ABの中点が で表されるのは、 2次元でも3次元でも、より次元が多くなっても変わりません。 また、円のベクトル方程式は で表されますが、 3次元では球面のベクトル方程式も同様に表されます。 つまり、 ベクトルを用いることによって、図形問題を扱いやすく、シンプルに表現できるようになる、ということです。 ベクトルの三角形の面積公式 三角形の面積は、ベクトルを用いて表現できます。 三角形の面積として、一番最初に習うのが でしょう。 図形の性質の単元で、 ヘロンの公式についても学習済みです。 三角形のそれぞれの辺を a, b, c とすると、 がヘロンの公式です。 ベクトルではこれに加えて、あと2つの三角形の面積の求め方を学習します。 三角形の面積については、これら 合計5つについて知っていれば十分です。 ベクトルを用いて、三角形の面積を表すには、 を利用します。 とおくと、 ですから、 ベクトルの内積が、 で表されます。 よってこのような式になります。 ここから、 となります。 ここであることに気が付いた人は、数学の力がある方です。 気が付かなかった方は、これから注意しましょう。 C 2＝D ですから、 だとしても とは限らないということです。 これが成立するためには、 でなければなりません。 合わせて、 であることも確認しておきましょう。 つまり、 を証明しなければなりません。 ですから、 となりますから、今回は問題ありません。 よって となります。 ここから、もう一つの公式を導出しましょう。 とすると、 から、 となります。 絶対値を付けるのを忘れないようにしてください。 この公式は、 2次元の座標平面上のベクトルにのみ成立するものですが、先にも申し上げたように、 は、より高次元のベクトルでも成立します。 ベクトルの円の面積公式 円の面積は、円の半径を rとすると、 で表されます。 円の面積を求めるときには大抵、半径を求めることになりますから、無理をしてベクトル表示にすることはありません。 円の中心と、円上の一点の座標がわかっているときには、半径 rが求まりますから簡単です。 円上の 3点がわかっているときには、円の方程式を求めることで円の中心を求め、そこから円の面積を求めるとよいでしょう。 どうしてもベクトルを使いたいという場合は、 ベクトルを使って円の中心を求めます。 3点を通る円の中心は、その 3点を頂点とする三角形の外心（外接円の中心）ですから、 3点の座標から外心の位置ベクトルを求めます。 ベクトルと面積のまとめ 最後までご覧くださってありがとうございました。 この記事では、ベクトルと面積についてまとめました。 三角形の面積は、 あるいは です。 また、平行四辺形の面積はこれらを 2倍して、 あるいは となります。 ちなみに ですから、「たすきに掛ける」ことさえ覚えていれば、どちらから引いても構いません。 ベクトルは扱えれば非常に便利な道具です。 また、 理系の学部に進もうという学生にとっては、多くの研究においても使う、非常に重要な概念ですから、しっかり勉強しておきましょう。 詳しくは大学に進学して「ベクトル解析」を受講してください。 ご参考になれば幸いです。

次の

【中学数学】平行四辺形の対角線、面積について。

次の平行四辺形の面積を求めましょう。 次に高さを考えましょう。 底辺に垂直なところが高さになるのは後ほど解説します。 先ほどの平行四辺形を切り貼りしてみましょう。 下の図のように、2つの直角三角形と長方形に分けてみます。 2つの直角三角形は合同です。 次にその一方の直角三角形を移動させてみます。 直角三角形を移動させてみると、平行四辺形が長方形になりました。 と、いうことは、平行四辺形の面積を求めるには、この長方形の面積を求めればいいということになります。 また、もとの平行四辺形の底辺と高さを書き入れてみます。 底辺と横は見た目で一致していることが分かります。 また、縦と高さの位置が一致しています。 三角形を切り取って平行四辺形を長方形にできないときはどうしたらいい？ 三角形を切り取って平行四辺形を長方形にできない平行四辺形とは下のような平行四辺形です。 この場合は少し視点を変えて考えてみるとうまくいきます。 今までのような面積の求め方とは見方を変えて、全体の面積から余分な面積を差し引いて、平行四辺形の面積を出してみます。 まずは平行四辺形を含む長方形を書いてみましょう。 下の図のようになればOKです。 長方形を作ることで、2つの直角三角形ができました。 この長方形の面積ははじめの平行四辺形に2つの直角三角形を足したものです。 このことを平行四辺形を中心に考えると、長方形の面積から2つの三角形の面積を引いたものだと分かります。 長方形から三角形2つの面積を引けば平行四辺形の面積になることは分かったので、今度は三角形の場所を変えてみます。 右側にある三角形を左側に寄せてみます。 このとき、残った右側の長方形 正方形っぽくもみえますが の面積は、長方形から2つの三角形を引いた面積です。 と、いうことは、この長方形の面積ともとの平行四辺形の面積は等しいということになります。 またこの長方形の縦の長さは平行四辺形の高さに、横の長さは底辺に当たります。 先に説明した平行四辺形の面積の説明も、この長方形から2つの三角形を差し引くという形で説明可能です。 ただ、直接面積を求める形ではないので、少し分かりにくいということもあるかもしれません。 そんなときは、図を中心に説明してあげるといいと思います。 しかし、平行四辺形を長方形に変えることで、長方形と同じように面積が求められることが分かれば、平行四辺形の底辺と高さの関係が直角ということも納得がいくのではないでしょうか。 もしお子さんが斜めの辺などを掛けてしまう場合などには面積の公式の理屈がしっかり分かると良いかもしれません。 周り道に見えますが、平行四辺形を長方形に変えることができるイメージを持っていると公式も忘れることも少なくなります。

次の

平行四辺形とは？定義・条件・性質や、面積の公式、対角線の角度の求め方などを徹底解説！

対応する辺と高さの組 公式の導き方 平行四辺形の面積を求める公式は、 平行四辺形の一部を移動させて長方形にし、この長方形の面積を求めることで導き出せます。 下の図のように、平行四辺形の一部を三角形に切り取って、移動させてみましょう。 この長方形の（たて）は高さに等しく、（よこ）は底辺の長さ等しいことが分かります。 …と、説明したものの、下のような平行四辺形だと、先ほどのように三角形をいい感じに切り取ることができませんね。 どうしたらいいでしょうか？ 適切な三角形を切り取れない こんなときは、いくつかの平行四辺形をくっつけてみてはどうでしょうか？とりあえず、3倍の大きさの平行四辺形を作って、最後にその面積を3分の1にする、という具合です。 この大きな平行四辺形の面積を3分の1にすると、結局 下の図に示した台形の面積を求めよ。 この問題では、2種類の辺の長さが与えられていますが、面積を求めるには、対応する高さが存在する辺を選ぶ必要があります。 今回、13 cm の辺に対する高さは分かりませんが、5 cm の辺に対する高さは 12 cm とわかります。 よって、この底辺と高さのペアを使って、面積を求めます。 公式の意味をきちんと理解して、図形から必要な長さを選べれば、計算自体は難しくないですね。

次の