[OPアンプ] 加算回路、減算回路(差動増幅回路): みズとおかズ
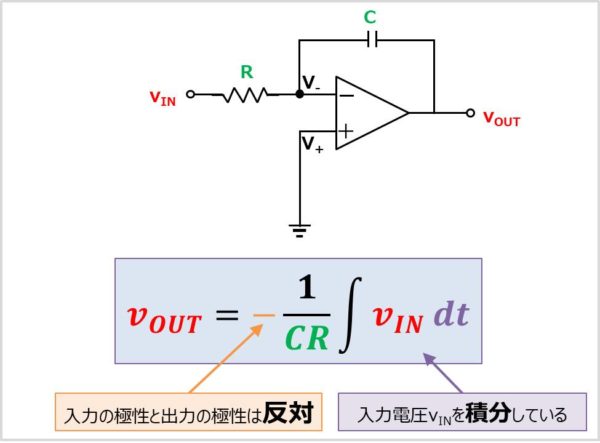
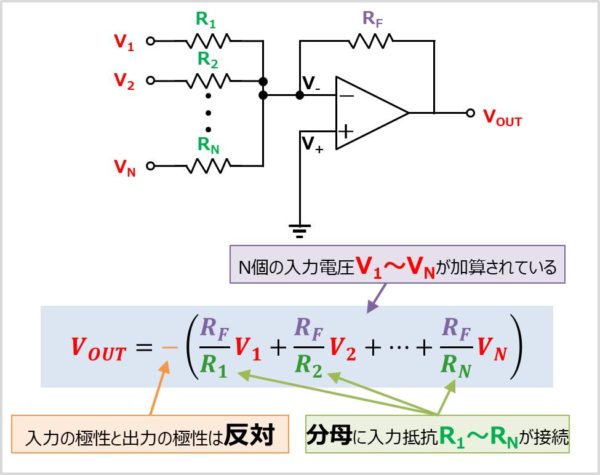
入力と出力の極性は 反対です。 なお、この加算回路は 反転増幅回路と回路が似ています。 以下の反転増幅回路と加算回路を示します。 そのため、 反転増幅回路を先に勉強すると、加算回路が理解しやすくなります。 反転増幅回路については以下の記事で詳しく説明しています。 加算回路の式の導出方法 加算回路の式の導出は以下の順序で行うと簡単に求めることができます。 この求め方はその他のオペアンプ回路 反転増幅回路など にも応用することができます。 このように、 短絡 ショート していないのに、常に2つの入力端子の電圧が同じになることからイマジナリショート 仮想短絡 と呼ばれています。 イマジナリショート 仮想短絡 は、 バーチャルショート、 仮想接地とも呼ばれています。 後日、イマジナリショートについて詳しく記事を書きます。 オペアンプは 入力インピーダンスが高いという特徴があります。 そのため、以下の式が成り立ちます。 そのため、以下の式が成り立ちます。 ここで 4 式を 2 式に代入すると、加算回路の式を求めることができます。
次の