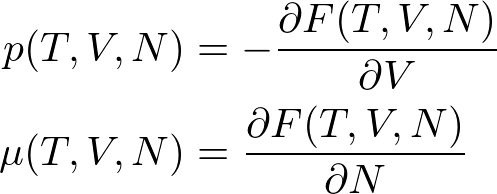ギブズ ヘルムホルツ の 式。 ヘルマン・フォン・ヘルムホルツ
電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)
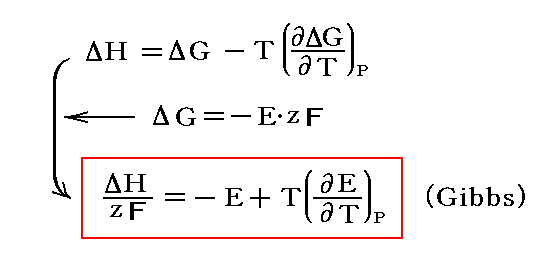
ギブズ-ヘルムホルツの式(ギブズ-ヘルムホルツのしき、 Gibbs-Helmholtz equation)とは、における関係式。 またはと、の間の関係式である。 1876年にが理論的に導出し、1882年にが実験的に証明した。 は1906年、この式を手掛かりにを発見した。 化学反応における温度依存性を考える上で重要な式である。 この式を使うと、のが温度によってどの程度変わるかを、から推定できる。 また、この式から導かれるを使うと、に達したときのとの存在比 が温度によってどの程度変わるかを、反応熱から推定できる。 反応熱が不明あるいは不確かなときは逆に、これらの熱力学関係式を使って反応熱を決定できる。 すなわちによる直接測定が困難な反応熱は、起電力やの温度依存性を測定することにより、間接的に測定できる。 の F が T と V の関数として表されているとき、この系の内部エネルギー U は次式で与えられる。 反応熱と自由エネルギー変化 [ ] 温度 T、圧力 p の定温定圧条件下で起こるを考える。 生成物のエンタルピー H products; T, p とギブズエネルギー G products; T, p の間にギブズ-ヘルムホルツの式が成り立つ。 これらもギブズ-ヘルムホルツの式と呼ばれる。 式の導出 [ ] 自由エネルギーの定義式からを消去すると、ギブズ-ヘルムホルツの式が得られる。 以下、ヘルムホルツエネルギーを例にとって説明する。 ギブズエネルギーに関してもほぼ同様の手順で導出できる。 熱力学ポテンシャル [ ] ヘルムホルツエネルギー [ ] 温度 T と体積 V を変数とするヘルムホルツエネルギー F T, V は、のひとつであり、系のにおける熱力学的性質の情報を全て持つ。 すなわち、関数 F T, V が T 0, V 0 で可能であれば、温度 T 0、体積 V 0 における S, p, U, G, H が全て計算できる。 ギブズエネルギー [ ] 温度 T と圧力 p を変数とするギブズエネルギー G T, p もまた熱力学ポテンシャルであり、系の平衡状態における熱力学的性質の情報を全て持つ。 すなわち、関数 G T, p が T 0, p 0 で可能であれば、温度 T 0、圧力 p 0 における S, V, H, F, U が全て計算できる。 エンタルピー [ ] 温度 T と圧力 p を変数とするエンタルピー H T, p は、熱力学ポテンシャルではない。 エンタルピーのは T, p ではなく S, p なので、 H T, p ではなく H S, p が熱力学ポテンシャルである。 温度 T 2、圧力 p におけるギブズエネルギー G を計算するには、 G T 1, p または S T 1, p と、 T 1 から T 2 の温度範囲にわたる H T, p が必要である。 化学ポテンシャル [ ] この節では、モルエンタルピーとの間に成り立つギブズ-ヘルムホルツの式について述べる。 単一成分系 [ ] のモルエンタルピー H m は、物質 1 あたりのエンタルピーであり、 H を n で割ったものに等しい。 理想希薄溶液 [ ] の定義には x i に基づくものや m i に基づくもの、 c i に基づくものなどいくつかのバリエーションがある。 を用いるのが便利である。 それに対して、現実の物理化学的な問題を扱う際には、質量モル濃度(溶質の物質量を溶 媒の質量で割ったもの)やモル濃度(溶質の物質量を溶 液の体積で割ったもの)が便利である。 この式から、理想希薄溶液の任意の成分の部分モルエンタルピー H i は組成 x には依らないことが分かる。 よって次式が成り立つ。 平衡の条件 [ ] 外界との間で物質の出入りがない、を考える。 温度 T 一定、圧力 p 一定の条件下で系がになるのは、ギブズエネルギー G が極小のときである。 より、可逆反応が起こるときの温度上昇 d T は、化学成分 A, B, C, D の物質量が固定されたときの温度上昇より小さくなければならない。 温度を下げたときは逆に、吸熱反応では生成物の量が減り、発熱反応では生成物の量が増える。 温度を変えたときに可逆反応がどちら向きに進むかは、ルシャトリエの原理と反応熱の符号から分かる。 しかし、反応がどの程度進むかについては、ルシャトリエの原理からは何もいえない。 燃料電池の起電力 [ ] を燃料とするの起電力の温度依存性は、水素のから計算できる。 229 V である。 脚注 [ ] 出典 [ ]• この比をと呼ぶ。 よって、熱力学第三法則に従う物質に限るならば、温度 T 2、圧力 p におけるギブズエネルギー G を関数 H T, p から計算できる。 とはみなせない、実在する溶液のこと。 参考文献 [ ]• ムーア『ムーア物理化学』上、藤代亮一 訳、、1974年、第4版。 ランドル『熱力学』ピッツアー、ブルワー改訂 三宅彰、田所佑士訳、岩波書店、1971年、第2版。 中村義男『化学熱力学の基礎』三共出版、1995年。 『化学熱力学講義』講談社、1981年。 玉虫伶太『活量とは何か』共立出版〈化学 One Point 1〉、1983年。 Frey、H. Strauss『』 PDF 計量標準総合センター訳、、2009年、第3版。 2017年9月13日閲覧。 デフェイ『化学熱力学』1、妹尾 学 訳、、1966年。 David W. Ball『ボール物理化学』上、田中一義、阿竹徹 監訳、、2004年。 関連項目 [ ]•
次の
ヘルムホルツエネルギーと最大仕事│大学の化学を探求する 大ケミ
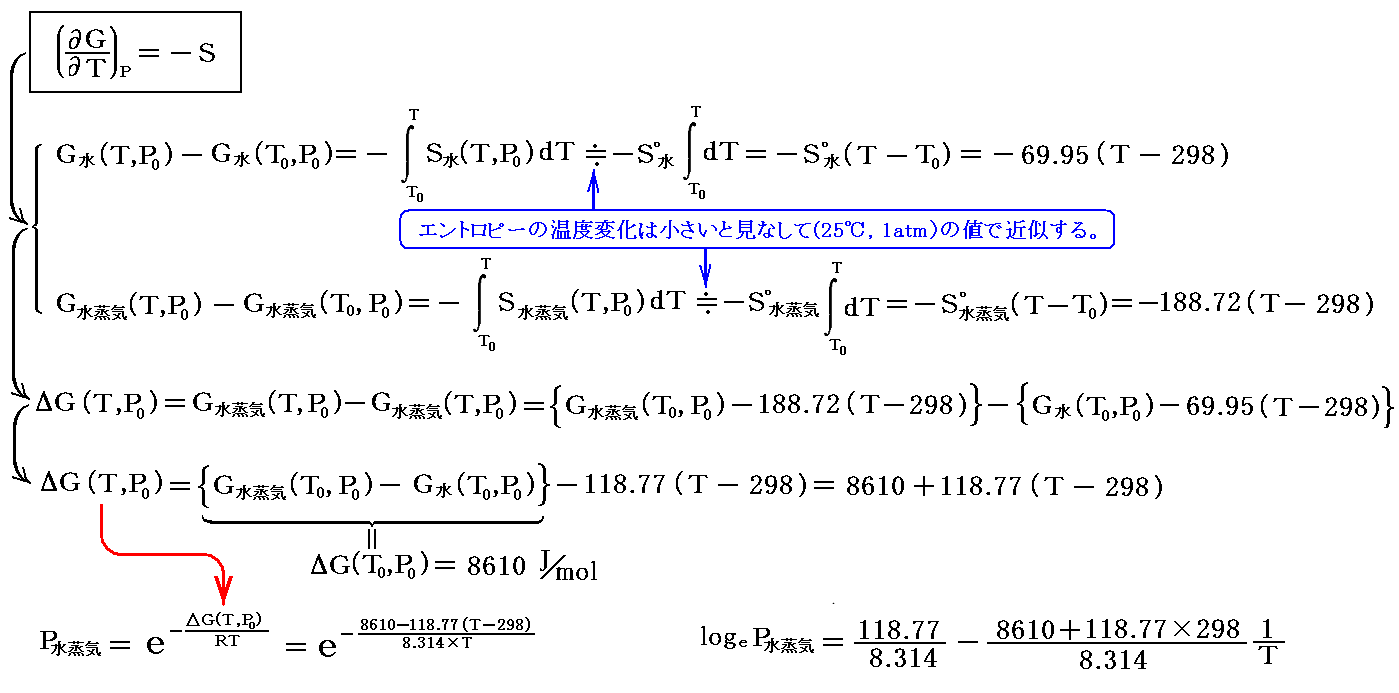
ギブズ-ヘルムホルツの式(ギブズ-ヘルムホルツのしき、 Gibbs-Helmholtz equation)とは、における関係式。 またはと、の間の関係式である。 1876年にが理論的に導出し、1882年にが実験的に証明した。 は1906年、この式を手掛かりにを発見した。 化学反応における温度依存性を考える上で重要な式である。 この式を使うと、のが温度によってどの程度変わるかを、から推定できる。 また、この式から導かれるを使うと、に達したときのとの存在比 が温度によってどの程度変わるかを、反応熱から推定できる。 反応熱が不明あるいは不確かなときは逆に、これらの熱力学関係式を使って反応熱を決定できる。 すなわちによる直接測定が困難な反応熱は、起電力やの温度依存性を測定することにより、間接的に測定できる。 の F が T と V の関数として表されているとき、この系の内部エネルギー U は次式で与えられる。 反応熱と自由エネルギー変化 [ ] 温度 T、圧力 p の定温定圧条件下で起こるを考える。 生成物のエンタルピー H products; T, p とギブズエネルギー G products; T, p の間にギブズ-ヘルムホルツの式が成り立つ。 これらもギブズ-ヘルムホルツの式と呼ばれる。 式の導出 [ ] 自由エネルギーの定義式からを消去すると、ギブズ-ヘルムホルツの式が得られる。 以下、ヘルムホルツエネルギーを例にとって説明する。 ギブズエネルギーに関してもほぼ同様の手順で導出できる。 熱力学ポテンシャル [ ] ヘルムホルツエネルギー [ ] 温度 T と体積 V を変数とするヘルムホルツエネルギー F T, V は、のひとつであり、系のにおける熱力学的性質の情報を全て持つ。 すなわち、関数 F T, V が T 0, V 0 で可能であれば、温度 T 0、体積 V 0 における S, p, U, G, H が全て計算できる。 ギブズエネルギー [ ] 温度 T と圧力 p を変数とするギブズエネルギー G T, p もまた熱力学ポテンシャルであり、系の平衡状態における熱力学的性質の情報を全て持つ。 すなわち、関数 G T, p が T 0, p 0 で可能であれば、温度 T 0、圧力 p 0 における S, V, H, F, U が全て計算できる。 エンタルピー [ ] 温度 T と圧力 p を変数とするエンタルピー H T, p は、熱力学ポテンシャルではない。 エンタルピーのは T, p ではなく S, p なので、 H T, p ではなく H S, p が熱力学ポテンシャルである。 温度 T 2、圧力 p におけるギブズエネルギー G を計算するには、 G T 1, p または S T 1, p と、 T 1 から T 2 の温度範囲にわたる H T, p が必要である。 化学ポテンシャル [ ] この節では、モルエンタルピーとの間に成り立つギブズ-ヘルムホルツの式について述べる。 単一成分系 [ ] のモルエンタルピー H m は、物質 1 あたりのエンタルピーであり、 H を n で割ったものに等しい。 理想希薄溶液 [ ] の定義には x i に基づくものや m i に基づくもの、 c i に基づくものなどいくつかのバリエーションがある。 を用いるのが便利である。 それに対して、現実の物理化学的な問題を扱う際には、質量モル濃度(溶質の物質量を溶 媒の質量で割ったもの)やモル濃度(溶質の物質量を溶 液の体積で割ったもの)が便利である。 この式から、理想希薄溶液の任意の成分の部分モルエンタルピー H i は組成 x には依らないことが分かる。 よって次式が成り立つ。 平衡の条件 [ ] 外界との間で物質の出入りがない、を考える。 温度 T 一定、圧力 p 一定の条件下で系がになるのは、ギブズエネルギー G が極小のときである。 より、可逆反応が起こるときの温度上昇 d T は、化学成分 A, B, C, D の物質量が固定されたときの温度上昇より小さくなければならない。 温度を下げたときは逆に、吸熱反応では生成物の量が減り、発熱反応では生成物の量が増える。 温度を変えたときに可逆反応がどちら向きに進むかは、ルシャトリエの原理と反応熱の符号から分かる。 しかし、反応がどの程度進むかについては、ルシャトリエの原理からは何もいえない。 燃料電池の起電力 [ ] を燃料とするの起電力の温度依存性は、水素のから計算できる。 229 V である。 脚注 [ ] 出典 [ ]• この比をと呼ぶ。 よって、熱力学第三法則に従う物質に限るならば、温度 T 2、圧力 p におけるギブズエネルギー G を関数 H T, p から計算できる。 とはみなせない、実在する溶液のこと。 参考文献 [ ]• ムーア『ムーア物理化学』上、藤代亮一 訳、、1974年、第4版。 ランドル『熱力学』ピッツアー、ブルワー改訂 三宅彰、田所佑士訳、岩波書店、1971年、第2版。 中村義男『化学熱力学の基礎』三共出版、1995年。 『化学熱力学講義』講談社、1981年。 玉虫伶太『活量とは何か』共立出版〈化学 One Point 1〉、1983年。 Frey、H. Strauss『』 PDF 計量標準総合センター訳、、2009年、第3版。 2017年9月13日閲覧。 デフェイ『化学熱力学』1、妹尾 学 訳、、1966年。 David W. Ball『ボール物理化学』上、田中一義、阿竹徹 監訳、、2004年。 関連項目 [ ]•
次の
ファントホッフの式
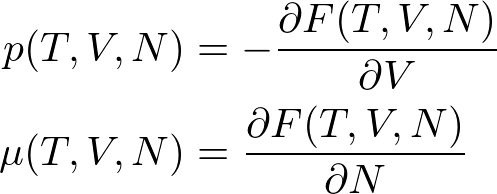
ギブズ現象(ギブズげんしょう,: Gibbs phenomenon)は、なのにおいて、その関数が discontinuity of the first kind 又は jump discontinuity となる点付近では、フーリエ級数の n 次が大きく振動して、部分和の最大値が関数自体の最大値より大きくなってしまうことがあるという振る舞いのことを指す。 この超過量は、高調波の(つまり、部分和の項数)が増えても無くならず、ある有限極限値に近付く。 日本語表記として「ギブズの現象」、「ギブス現象」、「ギブスの現象」とされることもある。 名称はにちなむ。 一般的には、大きさ a の跳びを有する、区分的連続微分可能な関数の任意の第1種不連続点において、その関数のフーリエ級数の n 次部分和( n は非常に大きいとする)は、跳びが起こる一方の端では、約 0. 089490... 不連続点自体では、フーリエ級数の部分和は、跳びの中点に収束していく(これは、元の関数がこの点で如何なる値を実際に取るかとは無関係である)。 ギブズ現象は、により、グラフ作成機において最初に発見された。 マイケルソンは、に、フーリエ級数を計算・再合成する機械的装置を開発したが、矩形波を装置に入力すると、グラフは、不連続点付近で行ったり来たりしようとするのだった。 これは、発生すると、の個数がに近付いても持続するようだった。 この現象を始めて数学的に説明したのが、 だった。 大まかな表現をするなら、この現象は、をである正弦波関数および余弦波関数からなる級数で近似することに内在する困難の現れである。 それは、また、ある関数のが次数の増大に応じて減衰していく仕方が、その関数の滑らかさに従うという原則に、緊密に関係している。 非常にでは、そのフーリエ係数は非常に急速に減衰する(そして、フーリエ級数は非常に急速に収束する)。 これに対し、不連続関数では、フーリエ係数の減衰は非常に緩やかである(従って、フーリエ級数の収束は非常に緩慢である)。 は、級数ではない程度の速さでしか減衰しない。 実際、上記のフーリエ級数は、変数 x の値で、するだけであることが分っている。 このことは、ギブス現象が何故起こるのかということの一端を説明する。 それは、絶対収束するフーリエ係数を有するフーリエ級数は、によりするから、上述のような振動を起こすことはありえないからである。 同じ理由で、不連続関数は、絶対収束するフーリエ係数を持つのは不可能である。 何故なら、もしそうした関数が存在したとしたら、それは、連続関数列の一様極限になるので、連続関数でなければならなくなり、矛盾が生じるからである。 実際上は、ギブズ現象による問題は、または Riesz summation 等のフーリエ級数の総和法における平滑化を行ったり、 ()を行ったりするなら、改善できる。 また、の代わりに、を用いるなら、ギブズ現象は発生しなくなる。 議論を単純にするため、 N が偶数の場合だけを扱うことにする(奇数の場合の議論も、全く同様にできる)。 このとき、 N 次部分和は次のようになる( N は偶数なので、この例では、 N 次高調波成分は存在しない)。 従って、次が得られる。 同様の計算で次が得られる。 Gibbs, J. , " Fourier Series". Nature 59, 200 and 606, 1899. 1955 , Trigonometrical series, Dover publications 第8章 第5節• Wilbraham, H. 1848 , On a certain periodic function, Cambridge and Dublin Math. , 3, pp. 198-201 関連項目 [ ]• - 多項式近似における問題• - のにおいて起きるこれと似たような現象 外部リンク [ ]• Braennlund, Johan, " ". Weisstein, Eric W. , " ". From MathWorld--A Wolfram Web Resource. Prandoni, Paolo, " ". Radaelli-Sanchez, Ricardo, and Richard Baraniuk, " ". コネクション・プロジェクト。 利用にはクリエイティブ・コモンズによる著作権帰属表示要。 Pavel, " ". math. mit. edu.
次の