ミンコフスキー時空のペンローズ図を描く
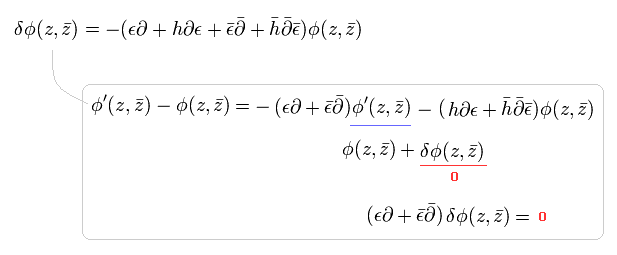
共形場理論 Conformal Field Theory for String Theory はじめに 2次元の場の理論である共形場理論は超弦理論の一部であるとともに,物性理論などに広く応用されている重要な理論である。 超弦理論の多くの公式は,共形場理論を用いると簡明に導ける。 そこで, 本ブログではR. Blumenhage, E. Plauschinn著,"Introduction to Conformal Field Theory with Applications to String Theory"の重要部分を解説する。 これを複素変数で表そう。 といえる。 Witt代数 上でみたように無限小変換はある開集合上で正則であればよいのだから,さらに拡張して,複素平面上で離散的な点を除いて 正則な有理型関数にまで拡張してよい。 次に生成子の従う代数を決定する。 このことから,以下のことがわかる。 代数の中心拡大は量子力学における射影表現と近い関係にある。 ここで,さらに構造 を加えよう。 次に,Jacobi恒等式を計算する。 さらに,以下のJacobi恒等式を計算する。 そして,その交換関係は以下で与えられる。 カイラル場のことを 正則場と呼ばれることが 主流である。 反カイラル場のことは 反正則場と呼ばれることが主流である。 無限小共形変換 無限小共形変換に対して,プライマリ場がどのように変換されるか調べてみよう。 エネルギー-運動量テンソル 通常,場の量子論では理論が備えているべき性質を持ったラグランジアンから出発する。 2次元の無限小変換の代数が無限次元であることから理論は強く拘束をうける。 とくに,理論に現れる作用の具体的な形を知らなくてもよくなる。 エネルギー-運動量テンソルの 振る舞いをみるだけで,必要な情報がえられるようになる。 共形不変性 共形場理論のエネルギー-運動量テンソルを求めるわけだが,場の量子論のNoetherの定理を思い出すとよい。 2次元ユークリッド空間に適用 2次元ユークリッド空間上の理論を複素変数で議論する。 以上から以下の結論を得る。 そして,演算子積による定式化を導入する。 場の量子論では,保存するチャージは対応する対称性変換の生成子と以下の関係にある。 場の量子論では相関関数に時間順序を導入していた。 これをRadial Orderingという。 反正則部も同様である。 ここで,交換関係を計算する。 この節では 厳密な 2点,3点関数を求める。 相関関数はOPEによって求められる。 共形Ward恒等式 場の量子論ではいわゆるWardは対称性の量子論的な現れである。 2次元の共形不変性から恒等式を求める。 2点,3点関数 本節では大域的共形対称性が2点,3点関数を決定することを示す。 3点関数 3点関数も同様に議論によって,以下の形に決まる。 ここから先は,長い計算の果てに以下の公式にたどり着く。 ローラン係数どうしの交換関係は長い計算の果てに以下のようになる。 応用4:カレント代数 本節ではいわゆるカレント代数について議論する。 反正則セクタについても同様である。 正規順序積 生成演算子を消滅演算子の左に持ってくる処方を正規順序積 Normal Ordering という。 本節ではOPEの非特異部が正規順序積を与えることを示す。 さらに考察を進めよう。 まず,以下の事実を示そう。 第二項についても同様に計算すると,以下の公式を得る。 よって,正規順序積はOPEの非特異部に 対応していることがわかる。 CFTの簡単な事例 これまではCFTの一般的な枠組みからわかることを紹介してきていた。 ここからは具体的な例にCFTを適用してみて,CFTの威力を理解してもらおう。 この理論ではスケールを規定する質量項がないため,共形 不変であることが期待される。 これを使った。 そのため,エネルギー-運動量テンソルを正規順序積に変形する。 反正則な部分についても同様である。 自由ボーズ粒子の作用は並進対称性を持っている。 ここでEuclid化するためにWick回転する。 次に共形次元を求めてみよう。 実際にこれを確かめてみよう。 最後にフェルミオン場の位相変換に関する変換性について議論する。 Laurentモードの代数は反交換関係となる。 これを計算してみよう。 以上から以下の事実がわかった。 エネルギー-運動量テンソルとセントラルチャージ ここでは,理論の詳細に立ち入らずにエネルギー-運動量テンソルを決めてみよう。 エネルギー-運動量テンソルがわかったところで,セントラルチャージを求めてみよう。
次の
