中学理科で習う『法則と原理の一覧』18個|中学試験・高校受験対策の要点まとめ

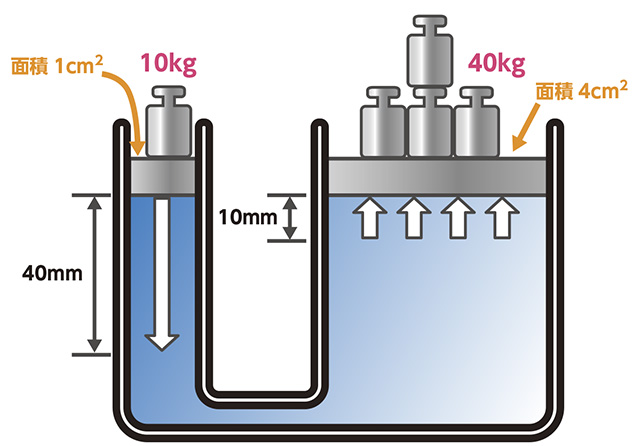
竹筒で出来ている水鉄砲についてピストンを押し込みます. その際に,先端だけでなく,側面にも穴をあけると,水の勢いはどうなるかという質問が,しばしば,中学校あたりの理科の問題で出題されますが,この場合,パスカルの定理により,筒の中のどの部分でも水圧は同じであるがために,水の勢いはどこでも同じというのが正解です. では,もし,水鉄砲を地面に向けてピストンを押し込んだ場合は,どのようになるでしょうか? やはり,水圧は同じということで,水の勢いはどの穴でも同じなのでしょうか? なぜ,これで混乱したかといいますと,例えば,縦方向に深い水槽に水を張った場合,水深が深くなればなるほど水圧は大きくなります. 例えば縦横高さがそれぞれ10mの水槽にいっぱいいっぱいに水を張った場合,水深5mの部分では,5mよりも浅い部分の水50トンの重さがかかり,水深10mの部分では,水100トンすべての重さがかかるために,水深が深いほど水圧が大きくなるという理解でよいのかと思います. 二つの例は,ピストンで圧力がかかるのか,水そのもので圧力がかかるのかという違いがありますが,どちらも同じようなものだと思います. 水鉄砲の中の水は水圧とは無関係なのでしょうか? なぜ,無関係ということができるのでしょうか? 混乱の原因はどこにありそうでしょうか? 教えていただきたく,よろしくお願いいたします. パスカルの原理ですが、 1・一定の「容器内部」に (=流体が流れていない) 2・非圧縮性流体を「満たして」 (容器内に空間が残っていない。 すなわち密閉されている。 ) 3・ある面に圧力をかけたとき、 (ある面とは、容器の面であればどこでもよい) 4・重力の影響が無ければ、つまり液面から同じ深さの地点同士ならば ・それらの点には等しい圧力が加わる です。 これら全部の条件を統合したのがベルヌーイの法則となります。 (流体の持つ、速度エネルギー・位置エネルギー・圧力エネルギー の合計が等しくなる。 ) ですので、水鉄砲の場合も、筒の下のほうに穴を開けた場合のほうが 水が勢いよく噴き出すことになりますが、圧力差があまりにも小さく無視しても問題ないので無視します。 なお、密閉について。 たとえば、プールの水は密閉されていないわけで、水面において圧力ゼロ(流体力学の場合、大気圧以外の圧力のみをカウントする) となるので、 「ピストンで押してもピストンが動くだけであり圧力は増えない」 という回答となります。 (水位差による圧力は考慮します。 ) 水面の圧力について tak0sanさんの、 >プールの場合も上から約101325Paの圧力をかけている >9800Paと101325Paを比べてみると無視できない量 というように、水面において大気圧をカウントする流儀もありますが、 その場合、 ・水面:101,325Pa ・水深1m:103125+9800=111,125Pa ・水深1m時点でも外から大気圧101,325Paで押されている。 と計算する必要があります。 結局、大気圧は差し引きゼロになるため計算上意味を持つことは 少ないのです。 (水を吸い上げる場合などには大気圧が意味を持つ。 ) ですので、9800Paと101325Paを比べるのはナンセンスです。 重力がある場合には気密系でも量が多ければ無視できません。 但し、通常の理科の実験で扱うような範囲では無視できる状態であると は思います。 プールの場合も上から約101325Paの圧力をかけているといえますが、 9800Paと101325Paを比べてみると無視できない量です。 パスカルの原理が成り立つのは穴が開いていない水槽の中です。 穴があって水が出るというのは流体だから質問のように穴の位置によって飛び出る水の位置は違います。 ただ横に長いホースの穴(例えば作物に水をやる場合)適度に間隔とって流せばほぼ等しく飛び出る。 ただこれも蛇口に近い側と中間と先端(行き止まり)で飛び出る水の勢いは差があるけど。 水を出すってことなら金魚の透明な袋に針で小さな穴開けて手で押しつぶす場合です。 ほぼ等しく圧力受けるので穴の大きさが同じなら上向きであろうと下向きであろうと勢いは同じ程度です。 質問の水鉄砲では穴の大きさが十分に小さく、穴の間隔が必要なだけ離れていれば上向きも下向きも同じです。 この回答への補足 ありがとうございました.「密閉しているか否か」がカギになってくるわけですね. では,水鉄砲の側面やホースに穴をあけた場合,厳密に考えれば,その時点で成り立たないと考えるべきだけれど,穴が十分に小さい場合は,穴が開いているための影響は無視できるだろうということなのでしょうか? 回答の中のホースの例で,「ただこれも蛇口に近い側と中間と先端(行き止まり)で飛び出る水の勢いは差があるけど。 まずNo. 4の方がおっしゃっているのは連続の式のことでベルヌイの式とは関係がありません。 非圧縮性流体とは密度が一定の流体のことを意味し、流れが速かろうが遅かろうが分子間の距離は一定のままです。 また分子間の距離は圧力とは関係がありません。 関係するのは温度です。 翼の説明に関して、No. 3の方が「翼の前面で分かれた空気は翼の後縁で一緒になります(これは厳密にいうと仮定でして、必ずしも一緒にならないこともあり得ます)。 」と書いておられますが、通常は上面の流れの方が後縁に先に達し、翼の後縁で一緒になることはありません。 A ベストアンサー こんにちは。 kgfはSI単位ではないですが、質量の数値をそのまま重さとして考えることができるのがメリットですね。 >>> ある試験片に40kgの重りをつけた時の荷重は何Nをかけてあげると、重り40kgをつけたときの荷重と同等になるのでしょうか? なんか、日本語が変ですね。 「ある試験片に40kgの重りをつけた時の引っ張りの力は何Nの力で引っ張るのと同じですか?」 ということですか? ・・・であるとして、回答します。 40kgのおもりなので、「おもりにかかる重力」は40kgfです。 重力は万有引力の一種ですから、おもりにも試験片にも、地球からの重力はかかります。 しかし、試験片の片方が固定されているため、見かけ、無重力で、試験片だけに40kgfの力だけがかかっているのと同じ状況になります。 98」でいいのでしょうか? いえ。 1kgf = 9.8N ですね。 力だけでなく、引っ張り応力を求めたいのでしょうか。 そうであれば、400Nを断面積で割るだけです。 こんにちは。 kgfはSI単位ではないですが、質量の数値をそのまま重さとして考えることができるのがメリットですね。 >>> ある試験片に40kgの重りをつけた時の荷重は何Nをかけてあげると、重り40kgをつけたときの荷重と同等になるのでしょうか? なんか、日本語が変ですね。 「ある試験片に40kgの重りをつけた時の引っ張りの力は何Nの力で引っ張るのと同じですか?」 ということですか? ・・・であるとして、回答します。 40kgのおもりなので、「おもりにかかる重力」は40kg... Q 片方の断面積が10平方cm、もう片方の断面積が5平方cmのU字管に水銀を満たすとどちらも同じ高さであった。 5平方cmの方に水100gを加えると断面積10平方cm側の液面がhcm上昇した。 このとき 1 断面積5平方cm側の水の高さは何cmか。 2 水銀の密度を13. 始めの液面から上昇した分の水銀の体積(断面積10側)と始めの液面と水銀までの水の体積が等しいということと、その高さでの圧力は等しいということから解いていくのがいいのでしょうか。 もし簡単に解けるような方法があれば教えていただけますか? おねがいします。 wikipedia. A8 後はこれを参考にしてください Q パスカルの法則では、密閉容器内の水に圧力を加えると、容器内の上下左右すべての面に、加えたものと同じ圧力が加わる、となっています。 ところで、仮定のはなしですが、配管が横方向に走っていて、配管の上下にそれぞれ圧力計が設置されていて、中を流れる水の圧力を測定しています。 圧力計は、導管で配管に接続されていて、配管からそれぞれ1m上または下の位置にあります。 また、配管および導管内は水で満たされているとします。 流体には、宇宙空間で自由落下しているのでない限り、重力が働きますから、密閉容器内部でも、場所によって圧力値は違います。 この圧力値に、圧縮分に見合った圧力増加が均等に加わるという意味だと思います。 >配管の上下にそれぞれ圧力計が設置されていて、中を流れる水の圧力を測定しています。 運動する流体の圧力とは、流体要素粒子の運動エネルギーから来る、流れる方向への力の単位面積当たりの値のはずです。 密閉容器内で、流体が運動するというのは、仰っておられるパイプの配管などのケースには当てはまらないはずです。 つまり配管パイプは、密閉容器でないはずです。 従ってパスカルの原理は、この場合、関係しないはずです。 >*上下の圧力計の測定値は、パスカルの法則のように、流水の圧力と同一になるのですか? 導管を設けることで、流れに攪乱がもたらされるはずです。 導管の形状や、配管との関係で、どういう流れの状態になるのか分かりませんが、同一にはならないはずです。 >*それとも、流水の圧力に導管の水頭圧を加えた値になるのですか? 重力水頭はこの場合、作用すると思いますが、上に述べたように、それ以外に流れの攪乱要因があり、例えば、導管内部では、流速が変化するはずです。 すると、当然、圧力も変化し、これは、導管や配管の形状や、流圧力によって変化するはずです。 流体の運動方程式を解かねばならないと思いますが、局所的にモデル化すれば解けるかも知れませんが、実際に導管を造って見て、シミュレーションする方が、どういう流れになるのか、また圧力はどうなるのか、よりはっきりと分かるはずです。 方程式では、なかなか解きにくいということです。 流体には、宇宙空間で自由落下しているのでない限り、重力が働きますから、密閉容器内部でも、場所によって圧力値は違います。 この圧力値に、圧縮分に見合った圧力増加が均等に加わるという意味だと思いま... A ベストアンサー No. 5です。 再度のチャレンジです。 奥行き1cm、幅1m、高さ2mの容器に水が入っています。 水の重さは簡単に計算できますが、あえて重さをm kg とします。 次に側面、即ちドアを置くべき場所に加わる力を考えます。 側面の最下部の一部分、幅1m、高さ1cmの面積だけに加わる力は、底面に加わるmg N よりもほんの少しだけ小さな力になります。 その1cm上の同じ面積に加わる力は、さらに又ほんの少し小さな値です。 しかし力は上に行くに従ってゼロに向かって小さくなりますので、力の総和は底面に加わる力の100倍になります。 即ち、ドアにかかる力は水の重さの100倍になるわけです。 何故このような結果になるのか、最初一瞬不思議でしたが、てこの原理のような理屈だろうと思った時、「パスカルの原理」を思い出しました。 油圧の原理となっている、あれです。 パスカルの原理はてこの原理のようなものですから、床を動かす場合と側面 ドア を動かす場合でエネルギーに損得があってはいけません。 次にこれを検証します。 簡単の為に蝶番は無視してドアは平行に動くものとします。 これが床面を動かしたことによる仕事と一致しているはずです。 これと同じ量のエネルギーがドアを開ける方向に使われたとします。 私としてはこれで解決ではないかと思いますが、いかがでしょうか。 5です。 再度のチャレンジです。 奥行き1cm、幅1m、高さ2mの容器に水が入っています。 水の重さは簡単に計算できますが、あえて重さをm kg とします。 次に側面、即ちドアを置くべき場所に加わる力を考えます。 側面の最下部の一部分、幅1m、高さ1cmの面積だけに加わる力は、底面に加わるmg N よりもほんの少しだけ小さな力になります。 その1cm上の同じ面積に加わる力は、さらに又ほんの少し小さな値です。 >これはどのような式なのでしょうか? 要するに、圧力差と流量は比例する、という式。 3の回答とは違います。 また、水の場合でも地下水(流速が遅く、かつ、管径が細い、と考えればよい)なら流速に比例します。 よって、油(など、粘性が高い流体)の場合の計算式がHPに示されていたものと思われます。 (圧力を、流体の密度で割ったもの。 ) L :管の延長 ただし、曲がりなどは、適当な倍率を掛けて直線に換算する。 g :重力加速度 約9. ) 、水の場合はfは定数(として解く場合と、Vの関数として解く場合の両方を使い分ける。 >できれば簡単な数値を入れて、計算式を教えて下さい。 動粘性係数とかレイノルズ数とか出てきて、とてもじゃないけど簡単じゃないです。 >これはどのような式なのでしょうか? 要するに、圧力差と流量は比例する、という式。 3の回答とは違います。 それ自体はそう... A ベストアンサー まずは問題を簡単にしてみましょう。 あるホースがあって、そのホースがつながっている蛇口は、何が何でも一定の水量の水が出てくるものとします。 そのホースの先に、断面積が半分の細いホースをつないでみましょう。 勿論水が漏れないようしっかりつなぎます。 すると、この細いホースを流れる水量は太いホースの水量にくらべ倍の速さで流れなければなりません。 つまり勢いが強くなった訳です。 断面積が半分になったので倍の速さで流れないと水量のつじつまが合わなくなってしまいますからね。 では、細いホースの先に、さらに元のホースと同じ太さのホースをつないでみましょう。 するとこの最後につけたホースに流れる水の速さは元に戻って、最初のホースと同じ速さになります。 川もだいたい同じですよね。 川幅が広いと流れは遅く、狭いと速くなります。 さて、これまではホースの抵抗を全く無視していましたが、ここからはより現実に近く考えてみましょう。 ホースの抵抗は細い程大きくなり、水が流れ難くなります。 水道の蛇口の部分では水の流れる経路を細く絞って抵抗を大きくしています。 その部分での流速は大きくなりますが、すぐに元と同じ大きさのパイプになりますので、もし抵抗が無いとすれば同じ水量が出てくるはずですが、実際には抵抗が大きなった分だけ水量が減ります。 さて、ご質問にあったホースで水まきをする時ですが、ホースの先を絞って、勢いを増す(流速を上げる)のが可能になるのは、絞ったからです。 もしこの絞った先に、同じホースをつなげたとしたら、最終的により少ない水量の水しか出てこないでしょう。 まずは問題を簡単にしてみましょう。 あるホースがあって、そのホースがつながっている蛇口は、何が何でも一定の水量の水が出てくるものとします。 そのホースの先に、断面積が半分の細いホースをつないでみましょう。 勿論水が漏れないようしっかりつなぎます。 すると、この細いホースを流れる水量は太いホースの水量にくらべ倍の速さで流れなければなりません。 つまり勢いが強くなった訳です。 断面積が半分になったので倍の速さで流れないと水量のつじつまが合わなくなってしまいますからね。 では、細...
次の