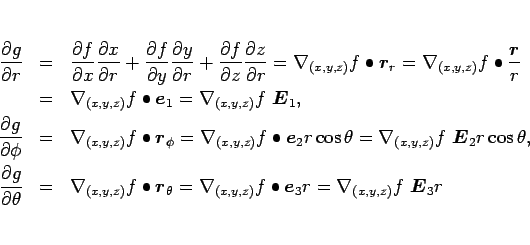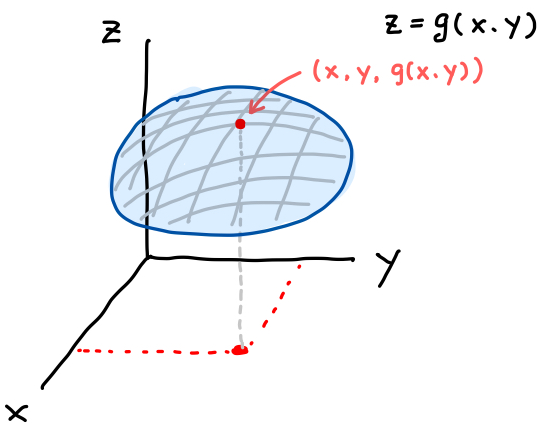
ベクトルの微分の定義 スカラを返す関数 において、ベクトル での微分係数は以下のように定義されます。 ベクトル , に対して、 ですから、式 1 の定義と、の式 5 より、 となることがわかります。 で微分すれば、その係数 のみ残りますので、解はk番目の成分が のベクトル、つまり になります。 2次形式の微分 次に2次形式 の微分を考えます。 はスカラになりますから、微分は式 1 の定義に従えばよいです。 行列Aを とすれば、 となりますから、 です。 ここでk番目の成分 での微分を考えると、積の微分公式より となります。 よって、 となります。 今回の式 2 、 8 は最小二乗法の解の導出に使用します。 関連：、 opabinia2.
次の
外積の図形的な意味 外積は， 与えられた2つのベクトルと直交し， 大きさが「もとの2つのベクトルが作る平行四辺形の面積」に等しい ようなベクトルであることが知られています。 それぞれ詳しく説明します。 という性質があります。 つまり、二つの空間ベクトルが与えられたとき、 それら両方ともに直交するベクトルを素早く求めるときに外積が使えるということになります。 という性質があります。 つまり、二つの空間ベクトルが与えられたとき、 それらが張る平行四辺形の面積を素早く求めるときにも外積が使えるということになります。 ベクトルの外積と内積の違い 外積は，2つのベクトルに対して ベクトルを対応させます。 内積は，2つのベクトルに対して スカラーを対応させます。 外積は，2つのベクトルが 両方とも三次元の場合にのみ定義されます。 内積は，2つのベクトルの 次元が等しければ何次元でも定義できます。 外積の微分公式 ベクトル解析の公式です（大学の力学、電磁気で使います）。 積の微分公式を使って成分ごとに計算すれば証明できます。 関連： 次回は を解説します。
次の
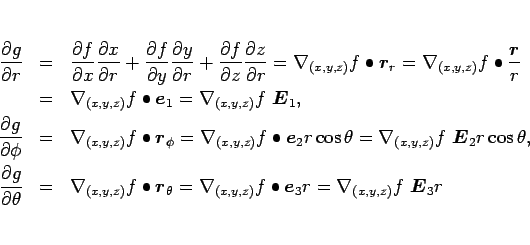
この記事にはやの一覧が含まれていますが、 によって参照されておらず、情報源が不明瞭です。 脚注を導入して、記事のにご協力ください。 多次元の領域上で定義されたに施すときには、の grad や、ベクトル場に対しては作用のさせ方により curl や div を与えたりする。 これらの形式的な積が、必ずしも他の作用素や積とであることは要求されない。 このような使い方をする最も一般的に知られる例は、、、、などであろう。 これは常に f の最も増加の大きい方向を指し、その点における最大増加率に等しい大きさを持つ（通常の微分と同様）。 特に、丘陵を平面上の高さ函数 h x, y として定めるとき、各地点での勾配を平面に射影したものは（地図上の矢印のような類で）各地点の最も傾きが急な方向を指す xy-平面上のベクトルとなり、勾配の大きさは、この最も急な傾きの値になる。 発散はベクトル場の指す方向にそれがどれくらい増加するかを大まかに測るものであるが、より精確にはその点での場の発散あるいは反発の傾向を測るものである。 各点における回転の値は、その点に中心を持つ小さな風車の軸周りのトルク（回転力）に比例する。 これは場 f の a 方向への変化量を与えるものである。 作用素の記法では、括弧に入れた要素は一つの一貫した単位と考えられ、この規約はでは（流体の「動く」微分としての）の言葉で縦横に用いられている。 ラプラス作用素 [ ] はベクトル場にもスカラー場にも施せるスカラー作用素である。 ラプラス作用素は現代的なに遍在しており、そのごく一部を挙げるならば、、、、などにおいて現れる。 この量は空間に対するベクトル場のの転置に等しい。 D, C, G, L, CC はそれぞれ divergence, curl, gradient, Laplacian, curl of curl を表す。 矢印は二階微分の存在を指し示すもので、青い円は curl of curl の中間表現、赤い（破線の）円は DD と GG が存在しないことを意味する。 そこでこの三種類の微分に、再び各種微分を施すと可能なものが五種類出てきて、これにとを加えると、以下のようになる。 参考文献 [ ]• Schey, H. 1997. Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. New York: Norton. Miller, Jeff, ,• Moler, Cleve January 26, 1998 , , netlib. org , 関連項目 [ ]• （） 外部リンク [ ]• 1994 Tai, Chen.
次の