ポアソン 分布 分散。 二項分布とポアソン分布の関係｜ポアソン分布で在庫数を考える

ポアソン分布とは何か。その性質と使い方を例題から解説 【馬に蹴られて死ぬ兵士の数を予測した数式】｜アタリマエ！

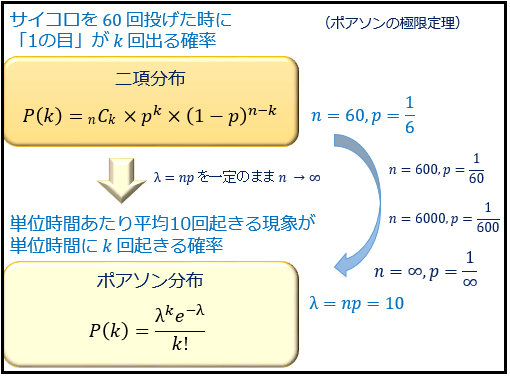
離散型の確率分布であり、二項分布の特別な場合の分布である ポアソン分布の概要や使い方についてまとめました。 二項分布はこちら： ～目次～ １. ポアソン分布の概要 ポアソン分布は、 二項分布において n 試行回数 が大きく、p 成功 発生 確率 が小さい場合の分布です。 ポアソン分布では、このnとpをまとめて とおき、一定の事象数や時間あたりの発生件数として使用します。 例えば、１年間の10万人あたりの交通事故の件数や、一定時間に窓口を訪れる人の数などが当てはまります。 他には、経済学者であるボルトキーヴィッチが馬に蹴られて死んだ兵士の数の規則性を発見した話が有名です。 この馬に蹴られて死んだ兵士の話を、上記のnとpに当てはめると以下になります。 ポアソン分布の確率密度関数 ポアソン分布の確率密度関数は以下になります。 この期待値 は、二項定理の期待値 と同様であることは理解しやすいかと思います。 期待値と分散からも二項分布と同等であることが分かります。 それぞれの計算方法は以下になります。 ポアソン分布の期待値の導出 次に上記の確率分布関数から期待値を求めます。 ・・・期待値の公式より ・・・ とする ここで、 は、 の公式そのものであるため、値を代入する。 ポアソン分布の分散の導出 以下の公式を使います。 まずは、上式の左項 を求めます。 ・・・期待値の公式より ・・・ とする ここで、まずは左項 を計算します。 ・・・ とする ・・・マクローリン展開の公式より 続いて、右項 を計算します。 ・・・マクローリン展開の公式より 以上から、以下が導出できました。 最後に、 に代入します。 以上となります。 ポアソン分布の期待値と分散の導出 モーメント 続いて、モーメント 積率母関数 を用いて期待値と分散を導出します。 モーメント関数の定義および公式は以下になります。 ・・・モーメント母関数 ポアソン分布のモーメント母関数 まず、ポアソン分布のモーメント母関数を求めます。 以上から、期待値は以下になります。 ポアソン分布のモーメント母関数の２回微分と分散 同様に、2回微分は以下になります。 以上から、分散は以下になります。 ポアソン分布のRでの扱い方 xを指定した時の事象の発生確率 dpois ポアソン分布をRで導出するにはdpois関数を使用します。 使い方は以下になります。

次の

コイン投げから分かる二項分布。正規分布やポアソン分布との関係性と近似について｜アタリマエ！

この性質から、ポアソン分布は二項分布の連続時間版と考えることができます。 718 はです。 By: ポアソン分布は、例えば「30分に平均2回電話がかかって来るコールセンターにおいて、1時間に6回電話がかかって来る確率」を求めるのに便利な分布です。 この場合、求めたいのは「1時間に6回電話がかかって来る確率」なので 「単位時間は1時間」・ 「k＝6回」となります。 104という値が求まりました。 これはつまり、「30分に平均2回電話がかかって来るコールセンターにおいて、1時間に6回電話がかかって来る確率は 約10. 4％である」ということを意味します。 これ、意外と高い確率ですよね。 ここから、「30分に平均2回しか電話がこないなら、1時間に6回も電話がかかってくることはないだろう」と 油断してはいけない、ということが分かります。 それがポアソン分布です。 使い道の広さと弱点 ポアソン分布は「事故の発生回数」や「サーバーへのアクセス数」など、様々なものに活用することができますが、使う上で1つ注意すべきことがあります。 それは、ポアソン分布は 「完全にランダムではない事象」に対しては正確な分析が出来ないという弱点を持っていること。 例えば先のコールセンターの例で言えば、「テレビで取り上げられた場合」には、たった1時間の間に普段では考えられないほど多くの問い合わせ電話がかかってくることが予想されますよね。 このように各事象の発生が完全にランダムというわけではなく、 他の事象発生との間に強い相関関係があるようなケースでは、ポアソン分布は機能しにくくなってしまうんです。

次の

ポアソン分布の当てはまりの改善方法 — ゼロから学んだまとめ

参考： ポアソン分布の導出 ポアソン分布を導出します。 つまり，以下の定理を証明します。 ここまで理解できればあとは計算するのみ。 極限のよい練習問題。 n-k! ポアソン分布と指数分布の関係 ポアソン分布は，ランダムなイベントの発生回数を表す分布でした。 ポアソン分布の確率変数は「回数」に対応するので，ポアソン分布は離散型確率分布です。 一方， 指数分布は，ランダムなイベントの発生間隔を表す分布です。 指数分布の確率変数は「時間」に対応するので，指数分布は連続型確率分布です。 前者は自明なので後者を証明します。 ポアソン分布の解析では指数関数のマクローリン展開が大活躍します。 ほとんど同様にしてできるので練習問題にどうぞ！.

次の